Andrea Moiola

Nel 2026-2027 Modellistica Numerica verrà tenuto da Andrea Bressan, Complementi di Matematica da Francesca Gardini e MNAPDE non sarà disponibile

Modellistica Numerica (matematica, laurea triennale):
Autunno 2025, 2024, 2023, 2022, 2021, 2020, 2019, 2018, 2017

Complementi di Matematica (ingegneria, laurea magistrale):
Autunno 2025, 2024, 2023, 2022, 2021, 2020, 2019

Metodi Numerici Avanzati per le Equazioni alle Derivate Parziali (matematica, laurea magistrale):
Primavera 2026, 2025, 2024, 2023, 2022, 2021, 2020, 2019

Spring 2016&2017: Numerical Methods for Financial Engineering (Henley Business School/ICMA centre)

Autumn 2013-2016: Vector Calculus (University of Reading)

• Since July 2020	Associate professor	University of Pavia	Department of Mathematics
• July 2017 - June 2020	Ricercatore (RTDB, equivalent to lecturer)	University of Pavia	Department of Mathematics
• March 2013 - June 2017	Senior research fellow (permanent post)	University of Reading	Department of Mathematics and Statistics
• March 2012 - February 2013	SNSF Fellowship	University of Reading	Supervised by Simon N. Chandler-Wilde
• Sept. 2008 - November 2011	PhD student / scientific assistant	ETH Zürich	SAM - Supervised by Ralf Hiptmair and Ilaria Perugia

CV - Curriculum Vitae (pdf)

ORCID ID:	0000-0002-6251-4440
MathSciNet:	931770
zbMATH:	moiola.andrea
DBLP:	75/9305
WoS ResearcherID:	K-6182-2015
Scopus Author ID:	37049069900
arXiv:	moiola_a_1
Iris:	11759
UniFind:	667588
Google Scholar:	jZXSlW0AAAAJ

• Numerical analysis, approximation of partial differential equations (PDEs) and integral equations
• Computational acoustics, electromagnetics and wave propagation
• Non-polynomial Trefftz-discontinuous Galerkin methods for time-harmonic problems: Helmholtz [1, 7, 9, 12, 14, T1, R3, R6, R8] and Maxwell [5] equations
• Polynomial quasi-Trefftz methods [29, 34, 37, R4]
• Approximation theory, in particular by plane waves and other non-polynomial functions [2, 3, 6, 8, 32, 40, R6, T1]
• Wavenumber-explicit analysis of time-harmonic boundary value problems, quasi-resonances, applications of Rellich- and Morawetz-type identities [4, 10, 20, 27, 31, R3]
• Coercive (sign-definite) formulations for wave problems [10, 19, 39, R4]
• Sobolev spaces on non-Lipschitz and fractal sets [15, 16, 17, 25], interpolation of Hilbert spaces [11]
• Scattering by non-Lipschitz and fractal obstacles, integral equations and numerical methods [24, 28, 35, 38 R5]
• Discrete dipole approximation (DDA) [21], hybrid numerical-asymptotic (HNA) boundary element methods [22], embedding formulae [R2], quasi-periodic problems [R3, R8]
• Space-time discretisations of evolution PDEs:
wave [13, 18, 23, 29, 36, 39, R7], Schroedinger [26, 30, 34], and heat [33] equations
DG [23], Trefftz DG [13, 18, 26, 30], quasi-Trefftz [29, 34], virtual element [33], and spline-based [36, 39, R7] discretisations, sparse grids [23, R7]

N. Galante, A. Moiola, E. Parolin,
Stable approximation of Helmholtz solutions in the 3D ball using evanescent plane waves,
SMAI J. Comput. Math., 11, 2025, pp. 435-472. DOI: 10.5802/smai-jcm.130 (open access). Preprint: arXiv:2401.04016, hal-04381632.
[ · evanescent-plane-wave-approximation on GitHub, implemented by Nicola Galante.]
P. Bignardi, A. Moiola,
A space-time continuous and coercive formulation for the wave equation,
Numerische Mathematik, 157(4), 2025, pp. 1211-1258. DOI: 10.1007/s00211-025-01478-3. Preprint: arXiv:2312.07268.
[ · CoerciveWaveTests on GitHub, implemented by Paolo Bignardi.]
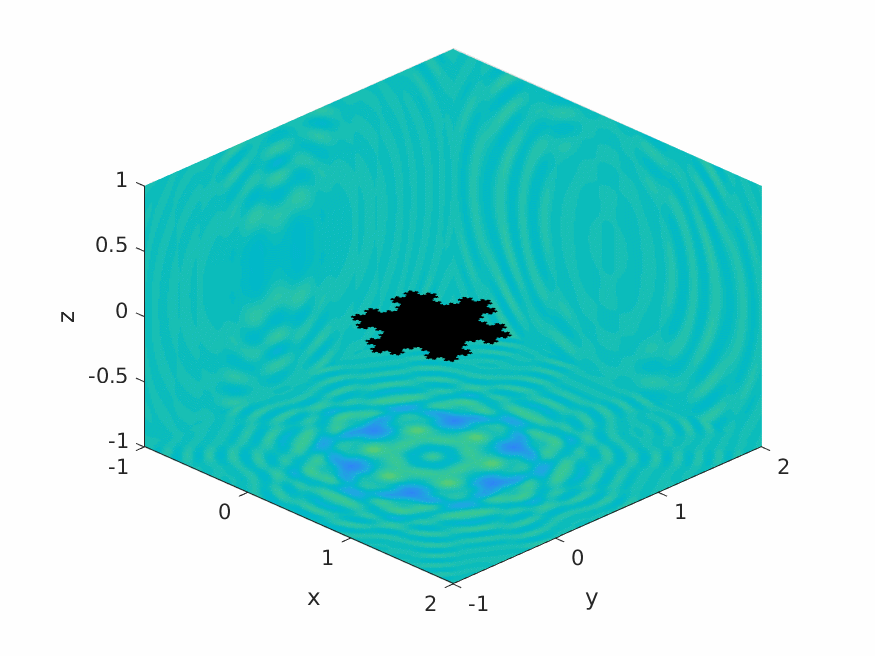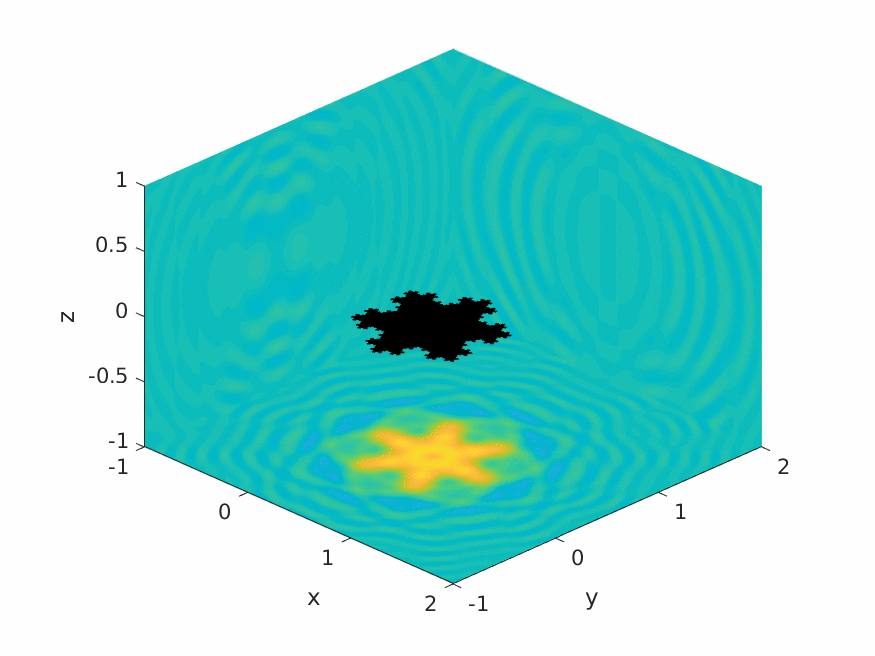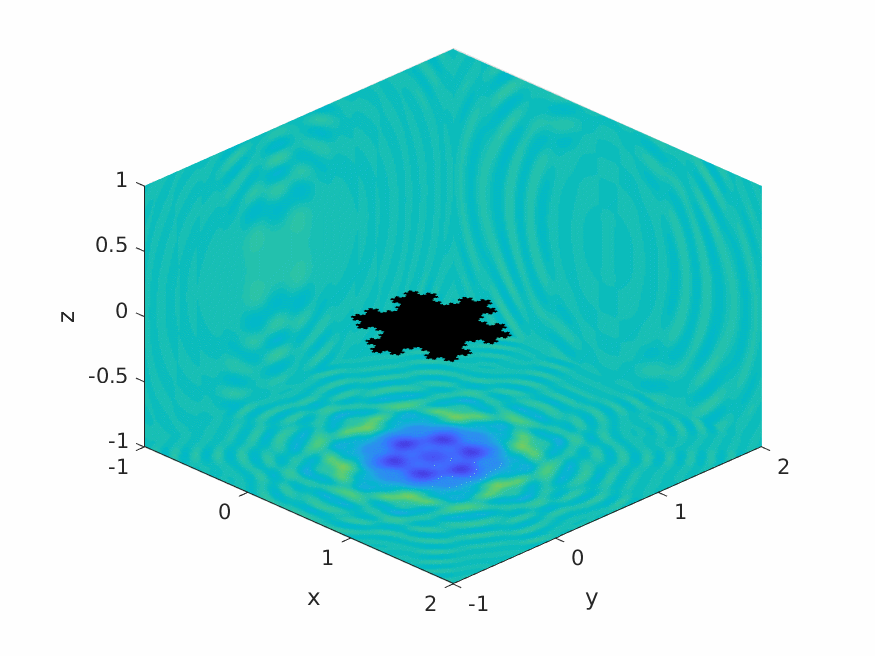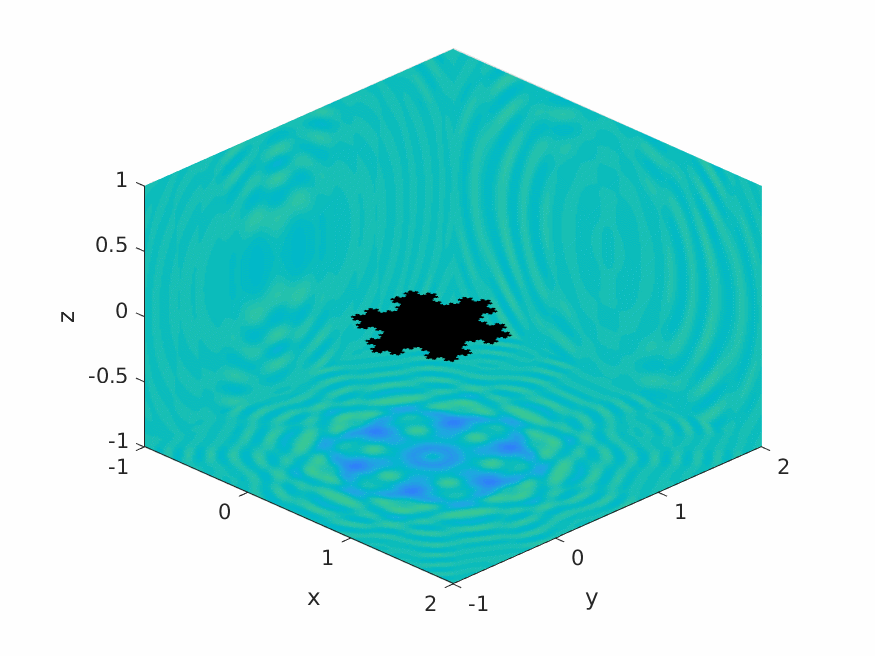
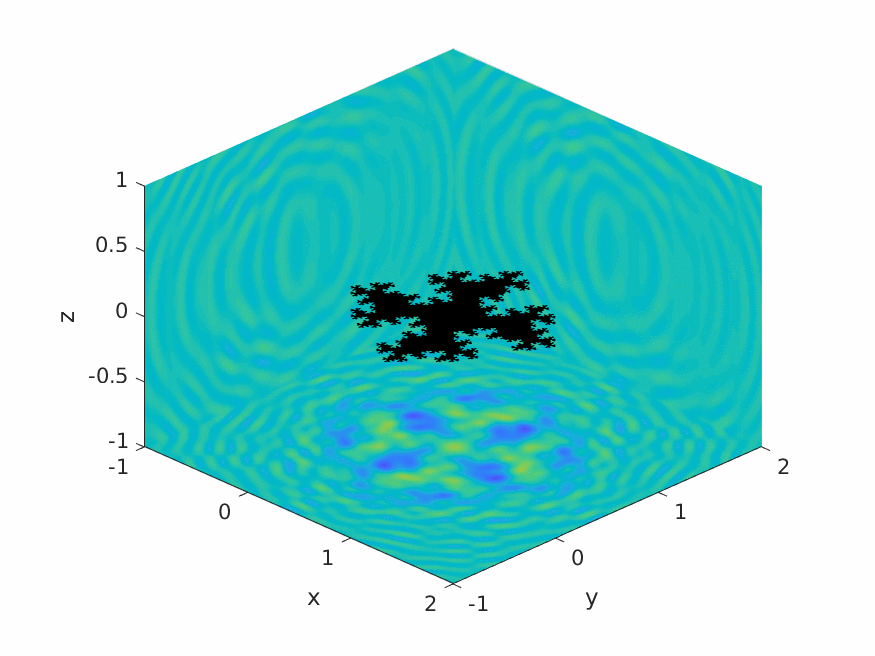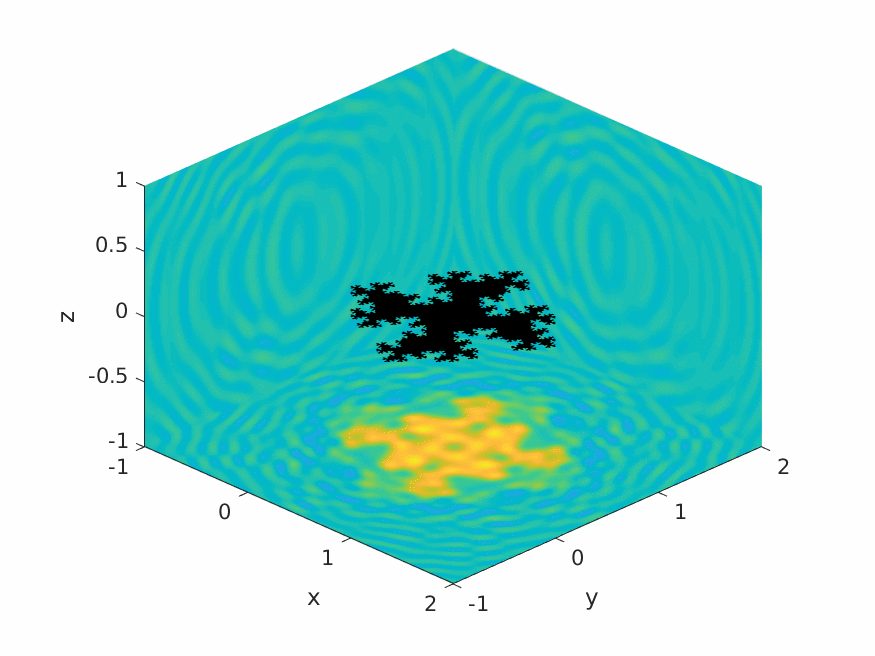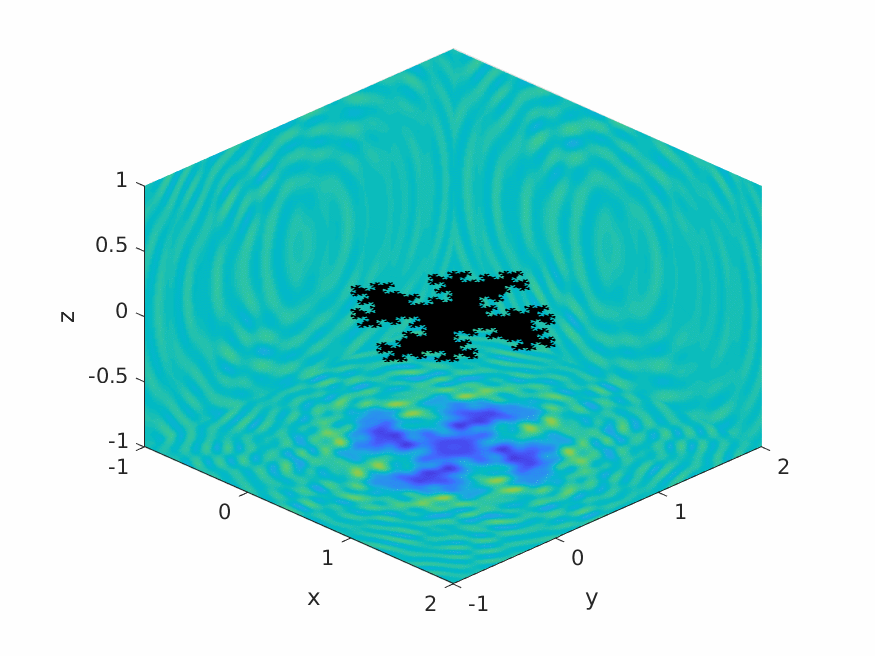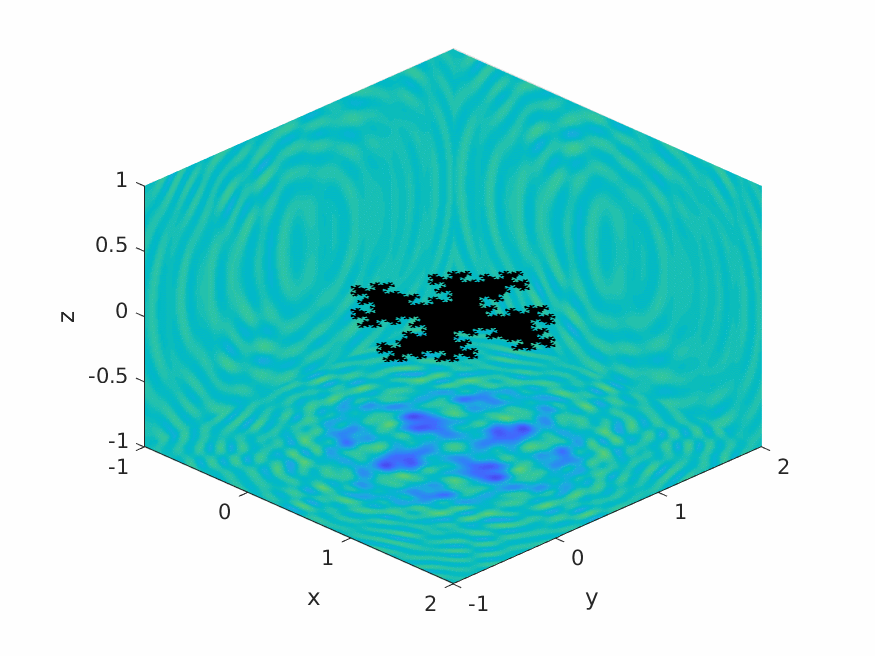
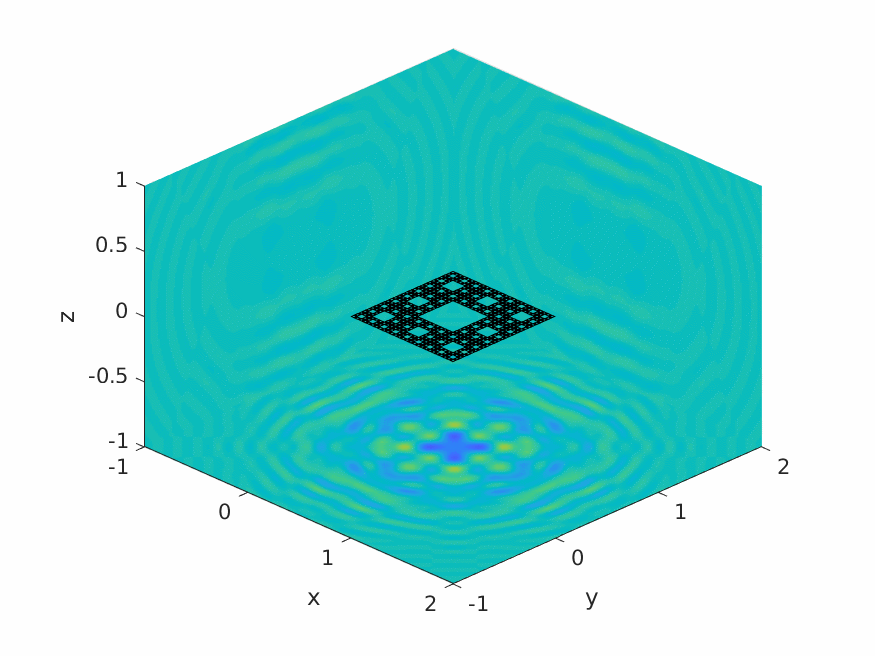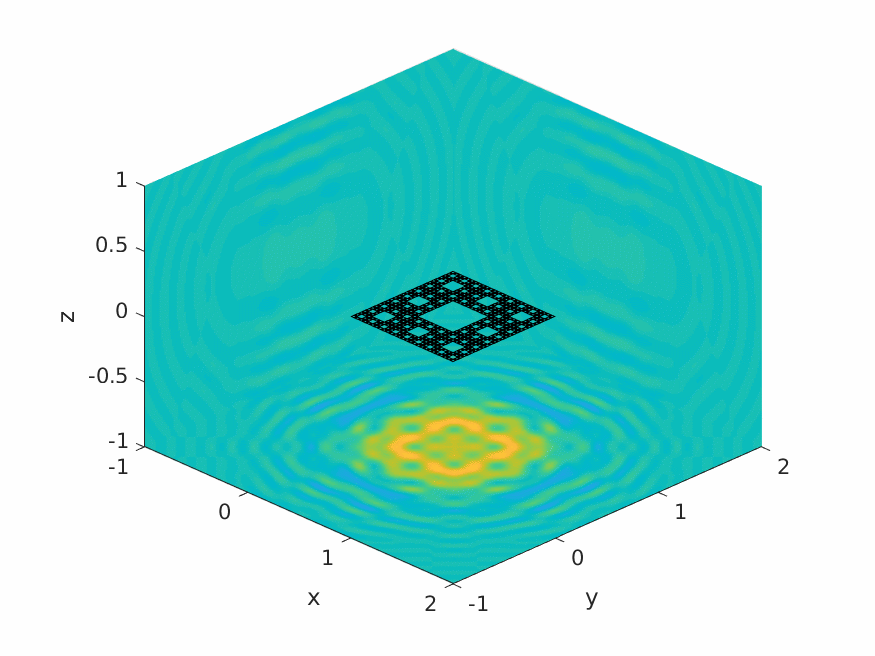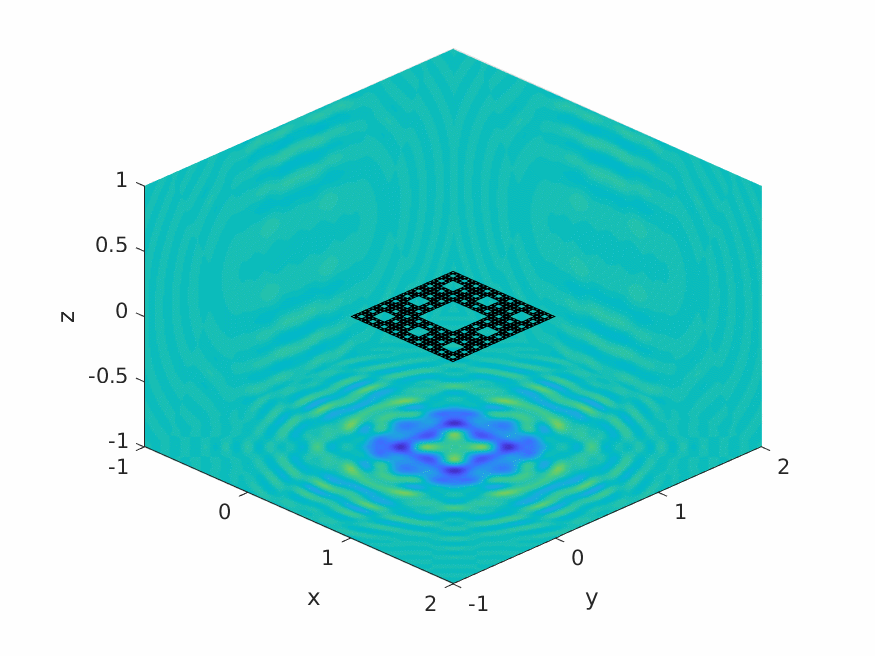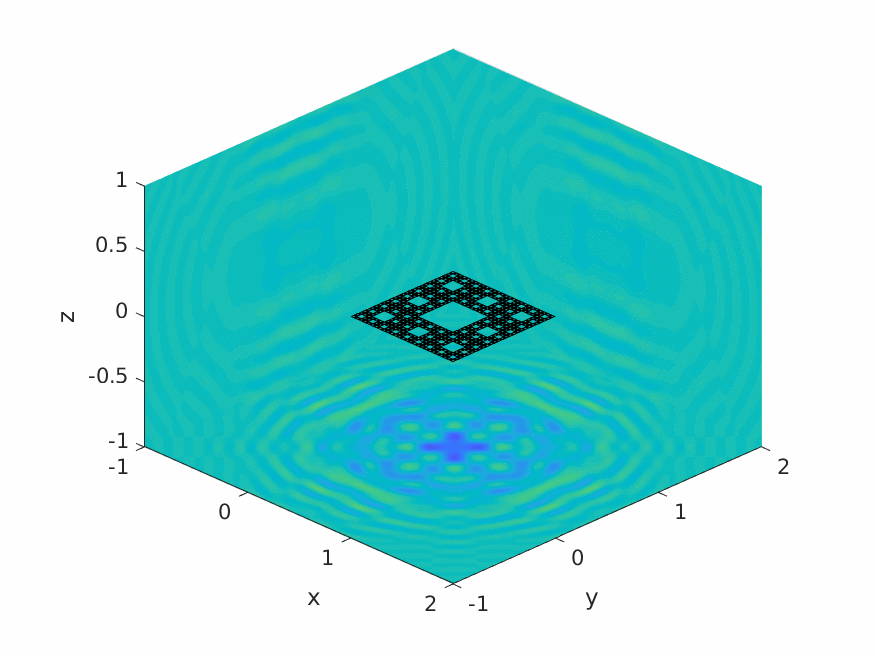
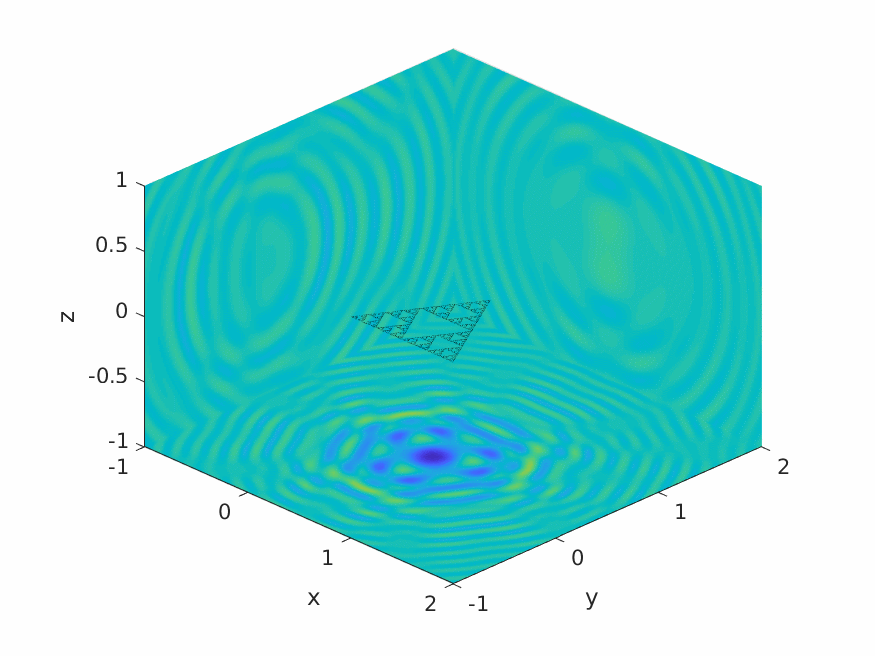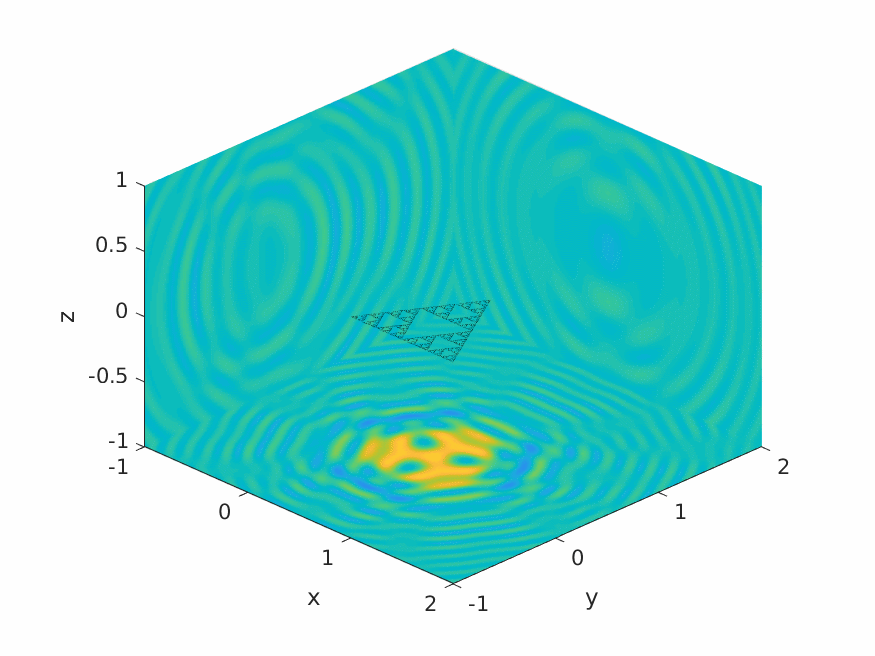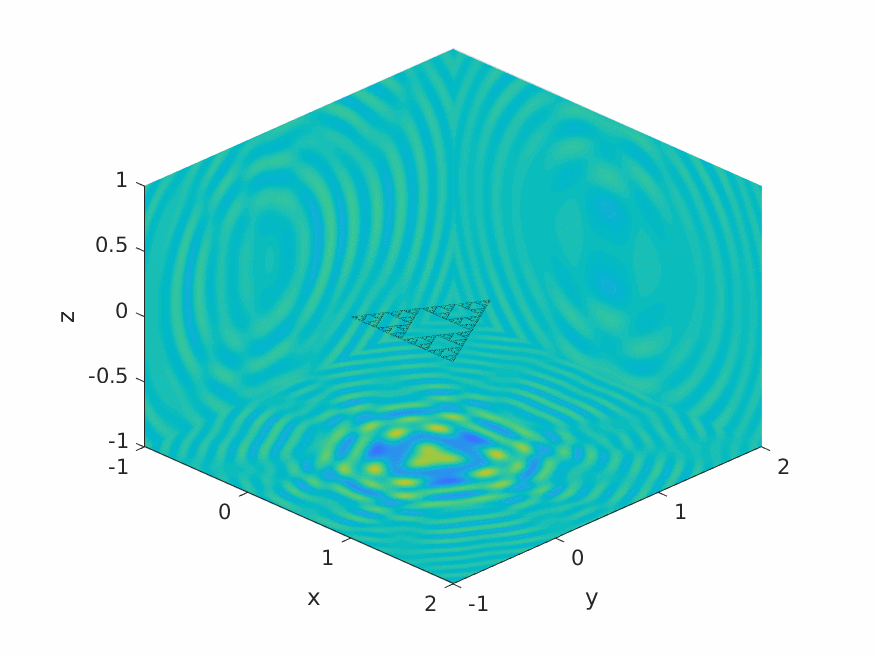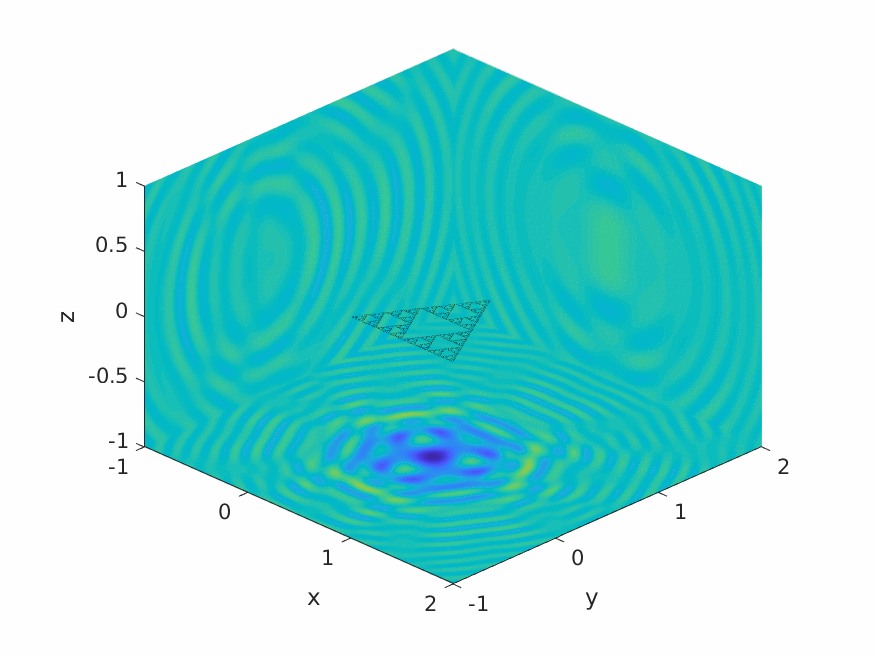
A.M. Caetano, S.N. Chandler-Wilde, X. Claeys, A. Gibbs, D.P. Hewett, A. Moiola,
Integral equation methods for acoustic scattering by fractals,
Proc. Roy. Soc. A (RSPA), 481 (2306), 2025, paper no. 20230650, 29pp. DOI: 10.1098/rspa.2023.0650 (open access). Preprint: arXiv:2309.02184.
[ · IFSintegrals on GitHub, implemented by Andrew Gibbs · Supplementary material]
L.-M. Imbert-Gérard, A. Moiola, C. Perinati, P. Stocker,
Polynomial quasi-Trefftz DG for PDEs with smooth coefficients: elliptic problems,
IMA J. Numer. Anal., 45(6), 2025, pp. 3473–3506. DOI: 10.1093/imanum/drae094 (free-access link). Preprint: arXiv:2408.00392.
[ · NGSTrefftz on GitHub · documentation · zenodo.12821320, implemented by Paul Stocker and Chiara Perinati.]
S. Fraschini, G. Loli, A. Moiola, G. Sangalli,
An unconditionally stable space-time isogeometric method for the acoustic wave equation,
Comput. Math. Appl. (CAMWA) 169, 2024, pp. 205-222. DOI: 10.1016/j.camwa.2024.06.009. Preprint: arXiv:2303.07268.
[ · XTIgA-Waves on GitHub, implemented by Sara Fraschini and Gabriele Loli.]
A.M. Caetano, S.N. Chandler-Wilde, A. Gibbs, D.P. Hewett, A. Moiola,
A Hausdorff-measure boundary element method for acoustic scattering by fractal screens,
Numerische Mathematik, 156(2), 2024, pp. 463-532. DOI: 10.1007/s00211-024-01399-7 (open access). Preprint: arXiv:2212.06594.
[ · IFSintegrals on GitHub, implemented by Andrew Gibbs.]
S. Gómez, A. Moiola,
A space-time DG method for the Schrödinger equation with variable potential,
Adv. Comput. Math., 50(15), 2024. DOI: 10.1007/s10444-024-10108-9 (open access). Preprint: arXiv:2306.05780.
S. Gómez, L. Mascotto, A. Moiola, I. Perugia,
Space-time virtual elements for the heat equation,
SIAM J. Numer. Anal. (SINUM), 62(1), 2024, pp. 199-228. DOI: 10.1137/22M154140X. Pdf file. Preprint: arXiv:2212.05343.
E. Parolin, D. Huybrechs, A. Moiola,
Stable approximation of Helmholtz solutions by evanescent plane waves,
Math. Model. Numer. Anal. (M2AN), 7, 2023, pp. 3499-3536. DOI: 10.1051/m2an/2023081 (open access). Preprint: arXiv:2202.05658.
[ · evanescent-plane-wave-approx on GitHub, implemented by Emile Parolin.]
T. Chaumont-Frelet, A. Moiola, E.A. Spence,
Explicit bounds for the high-frequency time-harmonic Maxwell equations in heterogeneous media,
J. Math. Pure. Appl. (JMPA), 179, 2023, pp. 183-218. DOI: 10.1016/j.matpur.2023.09.004 (open access). Preprint: arXiv:2301.07092, hal-04001866.
S. Gómez, A. Moiola, I. Perugia, P. Stocker,
On polynomial Trefftz spaces for the linear time-dependent Schrödinger equation,
Appl. Math. Lett., 146, 2023, 108824. DOI: 10.1016/j.aml.2023.108824 (open access). Preprint: arXiv:2306.09571.
L.M. Imbert-Gérard, A. Moiola, P. Stocker,
A space-time quasi-Trefftz DG method for the wave equation with piecewise-smooth coefficients,
Math. Comput., 92(341), 2023, pp. 1211-1249. DOI: 10.1090/mcom/3786. Preprint: arXiv:2011.04617.
[ · NGSTrefftz on GitHub, implemented by Paul Stocker.]
A. Gibbs, D.P. Hewett, A. Moiola,
Numerical quadrature for singular integrals on fractals,
Numer. Algorithms, 92, 2023, pp. 2071-2124. DOI: 10.1007/s11075-022-01378-9 (open access). Preprint: arXiv:2112.11793.
[ · IFSintegrals on GitHub, implemented by Andrew Gibbs.]
R. Hiptmair, A. Moiola, E.A. Spence,
Spurious quasi-resonances in boundary integral equations for the Helmholtz transmission problem,
SIAM J. Appl. Math. (SIAP), 82(4), 2022, pp. 1446-1469. DOI: 10.1137/21M1447052. Pdf file. Preprint: arXiv:2109.08530.
[ · Link to Matlab routine.]
S. Gómez, A. Moiola,
A space-time Trefftz discontinuous Galerkin method for the linear Schrödinger equation,
SIAM J. Numer. Anal. (SINUM), 60(2), 2022, pp. 688-714. DOI: 10.1137/21M1426079. Pdf file. Preprint: arXiv:2106.04724.
A. Caetano, D.P. Hewett, A. Moiola,
Density results for Sobolev, Besov and Triebel-Lizorkin spaces on rough sets,
J. Funct. Anal., 281(3), 2021, 109019. DOI: 10.1016/j.jfa.2021.109019. Preprint: arXiv:1904.05420.
S.N. Chandler-Wilde, D.P. Hewett, A. Moiola, J. Besson,
Boundary element methods for acoustic scattering by fractal screens,
Numerische Mathematik, 147(4), 2021, 785-837. DOI: 10.1007/s00211-021-01182-y (open access). Preprint: arXiv:1909.05547.
P. Bansal, A. Moiola, I. Perugia, Ch. Schwab,
Space-time discontinuous Galerkin approximation of acoustic waves with point singularities,
IMA J. Numer. Anal., 41(3), 2021, pp. 2056-2109. DOI: 10.1093/imanum/draa088 (free-access link). Preprint: arXiv:2002.11575.
A. Gibbs, S.N. Chandler-Wilde, S. Langdon, A. Moiola,
A high frequency boundary element method for scattering by a class of multiple obstacles,
IMA J. Numer. Anal., 41(2), 2021, pp. 1197-1225. DOI: 10.1093/imanum/draa025 (free-access link). Preprint: arXiv:1903.04449.
K. McCusker, C.D. Westbrook, A. Moiola,
Analysis of the internal electric fields of pristine ice crystals and aggregate snowflakes, and their effect on scattering,
Journal of Quantitative Spectroscopy and Radiative Transfer (JQSRT), 230, June 2019, pp. 155-171. DOI: 10.1016/j.jqsrt.2019.04.019.
A. Moiola, E.A. Spence,
Acoustic transmission problems: wavenumber-explicit bounds and resonance-free regions,
Math. Models Methods Appl. Sci. (M3AS), 29(02), 2019, pp. 317-354. DOI: 10.1142/S0218202519500106. Preprint: arXiv:1702.00745.
G.C. Diwan, A. Moiola, E.A. Spence,
Can coercive formulations lead to fast and accurate solution of the Helmholtz equation?,
J. Comput. Appl. Math. (JCAM), 352, 2019, pp. 110-131. DOI: 10.1016/j.cam.2018.11.035. Preprint: arXiv:1806.05934.
A. Moiola, I. Perugia,
A space-time Trefftz discontinuous Galerkin method for the acoustic wave equation in first-order formulation,
Numerische Mathematik, 138(2) 2018, pp. 389-435. DOI: 10.1007/s00211-017-0910-x (read online at this link). Preprint: arXiv:1610.08002.
S.N. Chandler-Wilde, D.P. Hewett, A. Moiola,
Sobolev spaces on non-Lipschitz subsets of Rⁿ with application to boundary integral equations on fractal screens,
Integr. Equat. Oper. Th. (IEOT), 87(2) 2017, pp. 179-224. DOI: 10.1007/s00020-017-2342-5 (read online at this link). Preprint: arXiv:1607.01994.
D.P. Hewett, A. Moiola,
A note on properties of the restriction operator on Sobolev spaces,
Journal of Applied Analysis, 23(1) 2017, pp. 1-8. DOI: 10.1515/jaa-2017-0001. Preprint: arXiv:1607.01741.
D.P. Hewett, A. Moiola,
On the maximal Sobolev regularity of distributions supported by subsets of Euclidean space,
Analysis and Applications, 15(5) 2017, pp. 731-770. DOI: 10.1142/S021953051650024X. Preprint: arXiv:1507.02698.
R. Hiptmair, A. Moiola, I. Perugia,
A survey of Trefftz methods for the Helmholtz equation.
In: Building Bridges: Connections and Challenges in Modern Approaches to Numerical Partial Differential Equations, Springer Lect. Notes Comput. Sci. Eng.,
edited by G.R. Barrenechea, F. Brezzi, A. Cangiani, E.H. Georgoulis, 2016, pp. 237-278. DOI: 10.1007/978-3-319-41640-3_8. Preprint: arXiv:1506.04521.
F. Kretzschmar, A. Moiola, I. Perugia, S.M. Schnepp,
A priori error analysis of space-time Trefftz discontinuous Galerkin methods for wave problems,
IMA J. Numer. Anal., 36(4) 2016, pp. 1599-1635. DOI: 10.1093/imanum/drv064. Preprint: arXiv:1501.05253.
R. Hiptmair, A. Moiola, I. Perugia,
Plane wave discontinuous Galerkin methods: exponential convergence of the hp-version,
Found. Comput. Math. (FoCM), 16(3) 2016, pp. 637-675. DOI: 10.1007/s10208-015-9260-1. Preprint: SAM Report 2013-31.
S.N. Chandler-Wilde, D.P. Hewett, A. Moiola,
Interpolation of Hilbert and Sobolev spaces: quantitative estimates and counterexamples,
Mathematika, 61(2) 2015, pp. 414-443. DOI: 10.1112/S0025579314000278. Preprint: arXiv:1404.3599.
Corrigendum: Mathematika, 68(4) 2022, pp. 1393-1400. DOI: 10.1112/mtk.12155.
A. Moiola, E.A. Spence,
Is the Helmholtz equation really sign-indefinite?,
SIAM Review (SIREV), 56(2) 2014, pp. 274-312. DOI: 10.1137/120901301. Pdf file. Preprint: MPS-2012-23.
C.J. Howarth, P.N. Childs, A. Moiola,
Implementation of an interior point source in the ultra weak variational formulation through source extraction,
J. Comput. Appl. Math. (JCAM), 27 2014, pp. 295-306. DOI: 10.1016/j.cam.2014.04.017. Preprint: MPS-2013-11.
R. Hiptmair, A. Moiola, I. Perugia, Ch. Schwab,
Approximation by harmonic polynomials in star-shaped domains and exponential convergence of Trefftz hp-dGFEM,
Math. Model. Numer. Anal. (M2AN), 48 (3) 2014, pp. 727-752. DOI: 10.1051/m2an/2013137 (free access). Preprint: SAM Report 2012-38.
R. Hiptmair, A. Moiola, I. Perugia,
Trefftz discontinuous Galerkin methods for acoustic scattering on locally refined meshes,
Appl. Numer. Math., 79 2014, pp. 79-91. DOI: 10.1016/j.apnum.2012.12.004. Preprint: SAM Report 2012-06.
A. Moiola,
Plane wave approximation in linear elasticity,
Appl. Anal., 92(6) 2013, pp. 1299-1307. DOI: link to journal. Preprint: SAM Report 2011-20.
R. Hiptmair, A. Moiola, I. Perugia,
Error analysis of Trefftz-discontinuous Galerkin methods for the time-harmonic Maxwell equations,
Math. Comput., 82(281) 2013, pp. 247-268. DOI: 10.1090/S0025-5718-2012-02627-5. Preprint: SAM Report 2011-09.
R. Hiptmair, A. Moiola, I. Perugia,
Stability results for the time-harmonic Maxwell equations with impedance boundary conditions,
Math. Models Methods Appl. Sci. (M3AS), 21(11) 2011, pp. 2263-2287. DOI: 10.1142/S021820251100574X. Preprint: SAM Report 2010-39.
A. Moiola, R. Hiptmair, I. Perugia,
Plane wave approximation of homogeneous Helmholtz solutions,
Z. Angew. Math. Phys. (ZAMP), 62(5) 2011, pp. 809-837. DOI: 10.1007/s00033-011-0147-y. Preprint: SAM Report 2009-27.
A. Moiola, R. Hiptmair, I. Perugia,
Vekua theory for the Helmholtz operator,
Z. Angew. Math. Phys. (ZAMP), 62(5) 2011, pp. 779-807. DOI: 10.1007/s00033-011-0142-3. Preprint: SAM Report 2009-27.
R. Hiptmair, A. Moiola, I. Perugia,
Plane wave discontinuous Galerkin methods for the 2D Helmholtz equation: analysis of the p-version,
SIAM J. Numer. Anal. (SINUM), 49(1) 2011, pp. 264-284. DOI: 10.1137/090761057. Pdf file. Preprint: SAM Report 2009-20.

Bib files: MathSciNet, zbMATH

A.M. Monforte, A. Moiola, S. Zanotto
Trefftz DG Approximation of the T-Matrix for Scattering by Periodic Layered Structures,
arXiv:2607.06475, 2026. [ · LayeredTMatrix on GitHub, implemented by Armando Monforte.]
M. Ferrari, A. Moiola, C. Perinati, I. Perugia
A space-time sparse-grid method for the wave equation,
arXiv:2606.09688, 2026. [ · Sparse-grid_XT_Wave on GitHub, implemented by Chiara Perinati and Matteo Ferrari.]
A. Moiola, N. Galante, E. Parolin
Trefftz methods with evanescent plane waves,
arXiv:2604.18175, 2026 (Waves 2026 abstract).
S. Gómez, D.P. Hewett, A. Moiola,
A discontinuous Galerkin method with fractal elements,
arXiv:2604.11093, 2026. [ · FractalDG on GitHub, implemented by Sergio Gómez.]
C. Perinati, L.-M. Imbert-Gérard, A. Moiola, P. Stocker,
A discontinuous Galerkin method for elliptic-hyperbolic equations,
arXiv:2604.06910, 2026. [ · TricomiDG.py · zenodo.18998988, implemented by Chiara Perinati.]
A. Moiola, A.M. Monforte,
Trefftz Discontinuous Galerkin methods for scattering by periodic structures,
arXiv:2505.23216, 2025. [ · DtN-TDG on GitHub, implemented by Armando Monforte.]
A. Gibbs, S. Langdon, A. Moiola,
Numerically stable computation of embedding formulae for scattering by polygons,
arXiv:1805.08988, 2018.
A. Moiola,
Trefftz-discontinuous Galerkin methods for time-harmonic wave problems,
PhD dissertation, Seminar for Applied Mathematics, ETH Zürich, 2011 (link to pdf, also available on the ETH e-collection), DOI: 10.3929/ethz-a-006698757.

• Pratyuksh Bansal, SCS
• Jeanne Besson
• Paolo Bignardi, RSE
• António M. Caetano, Universidade de Aveiro
• Simon N. Chandler-Wilde, University of Reading
• Théophile Chaumont-Frelet, INRIA, Lille
• Paul N. Childs, Roxar
• Xavier Claeys, ENSTA Paris
• Ganesh C. Diwan, Ultra Maritime
• Matteo Ferrari, Pavia
• Sara Fraschini, MoxOff
• Nicola Galante, INRIA, Paris
• Andrew Gibbs, UCL
• Sergio Gómez, Milano Bicocca
• David P. Hewett, UCL
• Ralf Hiptmair, ETH Zürich
• Charlotta J. Howarth
• Daan Huybrechs, KU Leuven
• Lise-Marie Imbert-Gérard, University of Arizona
• Fritz Kretzschmar
• Stephen Langdon, Brunel University London
• Francesca Locatelli
• Gabriele Loli, Pavia
• Lorenzo Mascotto, Milano Bicocca
• Karina McCusker, Meteorology, University of Reading
• Armando M. Monforte, Pavia
• Emile Parolin, INRIA, Paris
• Chiara Perinati, Pavia
• Ilaria Perugia, University of Vienna
• Giancarlo Sangalli, Pavia
• Sascha M. Schnepp
• Christoph Schwab, ETH Zürich
• Euan A. Spence, University of Bath
• Paul Stocker, University of Vienna
• Chris D. Westbrook, Meteorology, University of Reading
• Simone Zanotto, CNR-NANO, Pisa

PhD
• C. Perinati · Discontinuous Galerkin methods with Trefftz-type spaces · soon
• A.M. Monforte · Trefftz DG methods for periodic and multiple scattering problems · soon
• P. Bignardi · Space-time Morawetz formulations for the wave equation · 20.2.2025
• F. Locatelli · Exploring Local Discontinuous Galerkin methods for cross-diffusion systems: Towards complex multi-phase flow simulation · 4.2.2025
• S. Gómez · Nonconforming space-time methods for evolution PDEs · 22.2.2024 · ECCOMAS PhD Award
• K. McCusker · Fast, approximate methods for electromagnetic wave scattering by complex ice crystals and snowflakes · Reading, meteorology · 9.3.2020 · main supervisor C. Westbrook
• A. Gibbs · Numerical methods for high frequency scattering by multiple obstacles · Reading, maths · 26.4.2017 · co-supervised with S. Langdon and S.N. Chandler-Wilde

Master (Laurea Magistrale) · link to abstracts
• C. Perinati · A quasi-Trefftz DGM for the homogeneous diffusion-advection-reaction equation with piecewise-smooth coefficients · 9.2023 · arXiv:2312.09919
• A.M. Monforte · Plane wave discontinuous Galerkin methods for scattering by periodic structures · 9.2023 · arXiv:2312.12045
• N. Galante · Evanescent plane wave approximation of Helmholtz solutions in spherical domains · 4.2023 · co-supervised with E. Parolin · arXiv:2305.02175 · Con.Scienze national prize: best dissertation in mathematics
• S. Fraschini · Stability of space–time isogeometric methods for wave propagation problems · 7.2021 · co-supervised with G. Sangalli · arXiv:2303.15460 · Leslie Fox second prize 2025
• F. Locatelli · Migrazione di CO2 in strutture geologiche profonde: modelli e metodi numerici · 7.2020 · co-supervised with S. Manenti

The fields scattered by (pre)fractal sound-soft (Dirichlet) screens hit by acoustic time-harmonic plane waves.
The screens are: a Cantor dust, a Koch snoflake, a square snowflake, a Sierpinski carpet, a Sierpinski triangle, an "atomic" Sierpinski triangle, a Vicsek fractal.

• Dipartimento di Matematica, Università di Pavia
• Scientific Computing: Numerical Methods and Applications Group, Pavia
• IMATI - CNR (Istituto di Matematica Applicata e Tecnologie Informatiche), Pavia
• SIAM student chapter, Pavia
• International PhD program in Computational Mathematics, Learning, and Data Science, Università di Pavia + USI + FBK
• Joint PhD Program in Mathematics, Università di Pavia + Milano Bicocca + INdAM
• Very informal seminars, Università di Pavia + IMATI-CNR
• Applied maths seminars, Università di Pavia + IMATI-CNR
• Presidio della qualità di ateneo, Università di Pavia

Main grants:
• 2023-2025 PRIN grant: ASTICE - Advanced Space-TIme disCrEtization methods: theory, solvers and applications (PI)
Team members: Gabriele Ciaramella, Carlo Marcati, Lorenzo Mascotto, Ilario Mazzieri, Andrea Moiola
• 2023-2025 PRIN-PNRR grant: NOTES - Next generatiOn numerical Technologies for dEsign and Simulation
• 2019-2023 PRIN grant: NA_FROM-PDEs - Numerical Analysis of Full and Reduced order Methods for Partial Differential Equations
• 2020-2022 CE4WE - Circular Economy for Water and Energy
• 2016-2018 EPSRC 1st: Discretisations of sign-definite formulations for the Helmholtz equation (PI)
• 2012-2013 SNSF fellowship: Computational Wave Propagation (PI)

Previous affiliations:
• Department of Mathematics and Statistics, University of Reading
• Numerical Analysis and Computational Modelling Group, Reading
• MPE CDT, Centre of doctoral training Mathematics of Planet Earth, University of Reading and Imperial College London
• SAM - Seminar for Applied Mathematics, ETH Zürich

I'm member of:
• SIAM, Society for Industrial and Applied Mathematics
• GNCS, Gruppo Nazionale per il Calcolo Scientifico - INdAM
• UMI, Unione Matematica Italiana
• SIMAI, Società Italiana di Matematica Applicata e Industriale

2027
• Macquarie University, Sydney, July-September
• Oxford, May-June
• University of Vienna, March-April
• KU Leuven, January-February
2026
• Seminar, Institut Camille Jordan, Lyon, 10 November
• Seminar, LJLL, 2 November
• Seminar, POEMS team, Paris, 8 October
• ENSTA (UMA: team POEMS and team IDEFIX) and INRIA (team ALPINES), October-December
• Sabbatical leave, October 2026-September 2027
• Trefftz Workshop 1926-2026, Vienna 7-9 September
• CMAM, Computational Methods in Applied Mathematics, Vienna, 20-24 July
• Waves 2026, Montréal, 22-26 June
• LM day, Pavia, 22 May
• CompMat PhD Spring Workshop, Pavia, 20 May
• Théophile Chaumont-Frelet visiting, 16-20 February
• KU Leuven, 19-23 January
2025
• Astrid Herremans visiting, 17-21 November
• Basel, 14 November
• Interfaces and Unfitted Discretization Methods, Mittag-Leffler Institute, Stockholm, 2-9 November
• Nicola Galante and Emile Parolin visiting, 20-24 October
• Marcella Bonazzoli visiting, 30 September
• Enumath, Heidelberg, 1-5 September
• PoWER, Vienna, 2-4 July
• Vienna, 30 June-1 July
• DD29-Domain decomposition, MS on "Advanced space-time discretization methods: theory, solvers and applications", Milano, 23-27 June
• Summer stages "Matematica Attiva" for high-school students, Pavia 10-12 June
• CompMat spring workshop, Pavia, 23 May
• Numerical Analysis Research Cluster (NARC) seminar, University of Lagos, online, 21 May
• S.N. Chandler-Wilde visiting, 12-16 May
• LYNUM VII, Pavia, 7 May
• INRIA Paris, 31 March-4 April
• PhD viva of Paolo Bignardi, 20 February
• GNCS-SIAM Chapter Meeting, Pavia, 10-11 February
• Incontro Annuale dei Ricercatori in Matematica, Pavia, 5-6 February
• Numerical Methods and Techniques for Poroelasticity and Geomechanical Modeling, Milano, 5-6 February
• PhD viva of Francesca Locatelli, 4 February
• Advanced Solvers for Frequency-Domain Wave Problems and Applications, TSIMF, Sanya, 20-24 January
• Workshop on Hybrid numerical-asymptotic boundary element methods (HNA-BEM), Brunel, 9-10 January
• UCL, 7-8 January
2024
• Dave Hewett visiting, 4-8 November
• Nicola Galante and Emile Parolin visiting, 30 September-4 October
• Waves 2024, Berlin, 30 June-5 July
• Lions-Magenes days, Pavia (remotely), 21-22 May
• Contemporary Challenges in Trefftz Methods, from Theory to Applications, Casa Matemática Oaxaca (remotely), 12-17 May
• PhD viva of Sergio Gómez, 22 February
• Zurich, 30 January-1 February
• Incontro Annuale dei Ricercatori in Matematica, Pavia, 24-25 January
• Advanced numerical methods for non-local problems, Istanbul, 9-11 January
2023
• Boundary value problems and applications - The legacy of Enrico Magenes, Pavia, 21 November
• CANuTo23, Torino, 2-4 November
• Dave Hewett visiting Pavia, 16-20 October
• XXII Congresso UMI, Pisa, 4-9 September
• SIMAI, MS on "Space-time numerical methods and applications", Matera, 28 August-1 September
• PoWER 2023, Torino, 26-28 July
• Lise-Marie Imbert-Gérard visiting Pavia, 3-4 July
• Research in pairs, CIRM Trento, 25-30 June
• HOFEIM, Larnaca, 29 May-1 June
• CompMat PhD spring workshop, Pavia, 22 May
• Mathematical theory and applications of multiple wave scattering programme, INI Cambridge, 17 April-5 May
• Computational methods for multiple scattering workshop, INI Cambridge, 17-21 April
• Fractals in Pure and Applied Sciences, Roma, 15-17 March
2022
• Théophile Chaumont-Frelet visiting Pavia, 14-18 November
• At the Interface between Semiclassical Analysis and Numerical Analysis of Wave Scattering Problems, Oberwolfach, 25-30 September
• YAMC - Second Conference of Young Applied Mathematicians, Arenzano, 18-22 September
• Propagation of mechanical waves in deformable solids and meta-materials, Pavia, 5-9 September
• Waves 2022, Paris, 25-29 July
• Scattering and propagation of waves: theoretical and computational challenges, Reading, 27-29 June
• Solvers for frequency-domain wave problems and applications, Glasgow, 20-24 June
• UCL, 13-17 June
• MOX20, Milano, 27 May
• Visit and PDE afternoon, Vienna, 9-13 May
• Euan Spence visiting Pavia, 26-29 April
• Calcolo scientifico e modelli matematici: alla ricerca delle cose nascoste attraverso le cose manifeste, Roma, 6-8 April
• CIDMA Seminar, Aveiro/online, 17 March
• CompMat PhD Spring Workshop, Pavia, 16-17 March
• One World Numerical Analysis seminar, online, 21 February
• Mathematics of wave phenomena, online, 14-18 February
2021
• Scattering by random heterogeneous media, Augsburg, 13-15 September
2020
• PhD viva of Karina McCusker, Reading (remotely), 9 March
• Convegno GNCS, Montecatini, 11-13 February
• Structure, Regularity, and Robustness in the Approximation of Partial Differential Equations, Milano, 10 February
• PRIN meeting, Pavia, 27-28 January
• Daan Huybrechs visiting Pavia, 13-17 January
2019
• Andrew Gibbs visiting Pavia, 11-15 November
• Paul Stocker visiting Pavia, from October
• XXI Congresso UMI, Pavia, 2-7 September
• Waves 2019, MS on "Analysis and numerical methods for wave problems in heterogeneous media and complicated domains", Vienna, 25-30 August
• ICIAM, Valencia, 15-19 July
• Zurich, 24-28 June
• Mafelap 2019, Brunel University, London, 17-21 June
• HOFEIM 2019, Pavia, 28-31 May
• Roma, 13-16 May
• TiciNUM, Pavia, 10 May
• Computational mathematics, statistics and machine learning, Pavia, 7-9 May
• Informal seminar at IMATI-CNR, Pavia, 12 April
• Pontificia Universidad Católica de Chile, Santiago, 4-8 February
• WONAPDE 2019, Universidad de Concepción, Chile, 21-25 January
• University of Bath, 7-11 January
2018
• Seminar at Oldenburg University, 15 November
• Carlos Jerez-Hanckes visiting Pavia, 23-25 October
• Numerical Analysis of Complex PDE Models in the Sciences, ESI thematic programme, Vienna, 25 June-20 July
• Seminar at the University of Bologna, 20 June
• Reading, 4-8 June
• Zurich, 29 May-1 June
• Inverse Problems: Modeling and Simulation, Malta, 21-25 May
• Reading, 23-27 April
• Dave Hewett visiting Pavia, 16-19 April
• Seminar at SBAI, Sapienza, Roma, 21 March
• Euan Spence visiting Pavia, 12-16 February
2017
• IGA 2017, International Conference on Isogeometric Analysis, Pavia, 11-13 September
• IperPV2017, the XVII Italian Meeting on Hyperbolic Equations, Pavia, 6-8 September
• Equadiff 2017, Bratislava, 24-28 July
• Poems, Polytopal Element Methods in Mathematics and Engineering, Milano, 5-7 July
• 7th meeting of the Reading-Bath-Cardiff network on generalised solutions for nonlinear PDE, Reading, 13 June
• PhD viva of Andrew Gibbs, 26 April
• Workshop on Wave propagation in complex domains, UCL, 30 March
• Oberwolfach workshop on Space-time Methods for Time-dependent Partial Differential Equations, 12-18 March
• Mathematics in the Spirit of Joe Keller, Turing Gateway to Mathematics, Cambridge, 2-3 March
• International Conference on Domain Decomposition methods, DD XXIV, Svalbard, 6-10 February
2016
• Space-Time Methods for PDEs, RICAM, Linz, 7-11 November
• Seminar at SAM, ETH Zurich, 2 November
• PDE seminar at Reading, 18 October
• Mathematical and Computational Aspects of Maxwell's Equations, Durham, 11-21 July
• Modern Topics in Nonlinear PDEs and Geometric Analysis, LMS-CMI Research School, 4-8 July
• Seminar at Hamburg University of Technology, 24 June
• Mafelap 2016, Brunel University, London, 14-17 June
• ReaDG 2016: Recent advances in discontinuous Galerkin methods, Reading, 13 June
• Computational and Numerical Analysis of Transient Problems in Acoustics, Elasticity, and Electromagnetism, Banff International Research Station, 17-22 January
2015
• Seminar at Laboratoire Poems, ENSTA-INRIA-CNRS, Palaiseau, France, 18 November
• New directions in numerical computation, Oxford, 25-28 August
• Waves 2015, MS on "Wave-based discretizations", Karlsruhe, 20-24 July
• XXIV CEDYA / XIV CMA, special session on Computational Acoustics, Cadiz, 8-12 June
• Seminar at the University of Durham, 29 April
• Lions-Magenes days, Pavia, 13-14 April
• Seminar at the University of Bath, 20 February
2014
• Boundary and finite element methods for high frequency scattering problems, Reading, 15-16 December
• ReaDG: Recent advances in discontinuous Galerkin methods, Reading, 11-12 September
• Building Bridges: Connections and Challenges in Modern Approaches to Numerical PDEs, Durham, 8-16 July
• 3rd International Conference on Neural Field Theory, Reading, 16-18 June
• CIME course on Computational Electromagnetism, Cetraro, 9-14 June
• Computational mathematics and applications seminar, Oxford, 15 May
• Seminar at the University of Vienna, 24 March
• Recent Advances in Nonlinear PDEs and Calculus of Variations, Reading, 12-14 February
• British Computational PDEs Colloquium: New Trends, ICMS, Edinburgh, 23-24 January
2013
• Analysis of Partial Differential Equations, symposium in honour of Vladimir Maz'ya, Liverpool, 16-17 December
• Numerical analysis and data assimilation research afternoon, Reading, 30 October
• Seminar at the Brain Embodiment Lab, Reading, 25 September
• From Spectral Gaps to Particle Filters workshop, Reading, 17-18 September
• Data Assimilation and Inverse Problems summer school, Reading, 22-26 July
• CNS 2013 Computational Neurosciences Meeting, Paris, 13-18 July
• LMS-EPSRC short course on Modern Nonlinear PDE Methods in Fluid Dynamics, Reading, 8-12 July
• NETT Neural Engineering summer school, Nottingham, 1-5 July
• Mafelap 2013, Brunel University, London, 11-14 June
• Waves 2013, Gammarth, Tunisia, 3-7 June
• Meeting on Riemann-Hilbert problems and their applications, Reading, 29-30 May
• Seminar at the Collège de France, Paris, 17 May
• Oberwolfach workshop on Computational Electromagnetism and Acoustics, 20-26 January
• SIAM-UKIE annual meeting, Reading, 8 January
2012
• Reading departmental analysis day, Reading, 19 October
• Seminar at the University of Leicester, 18 October
• InnoWave conference, Nottingham, 3-7 September
• Zürich Summer School 2012 on A Posteriori Error Control and Adaptivity, Zürich, 20-24 August
• Mathmondes 2012, French-British Network on Waves, Reading, 9-10 July
• Conference in honour of Nancy Nichols' 70th birthday, Reading, 2-3 July
• ESCO2012, 3rd European Seminar on Computing, Pilsen, Czech Republic, 25-29 June
• ICMS Workshop on Boundary Value Problems for Linear Elliptic and Integrable PDEs, Edinburgh, 28 May-1 June
• Second international conference on Neural Field Theory, Reading, 19-21 April
• Seminar at the University of Strathclyde, Glasgow, 17 April
• Numerical analysis postgraduate seminar day, Reading, 30 March
• Seminar at the University of Bath, 23 March
• Seminar at the University of Reading, 12 March
• LNCC Petrópolis, 23-27 January
2011
• Workshop on Wave Propagation and Scattering, Inverse Problems and Applications in Energy and the Environment, RICAM Linz, Austria, 21-25 November
• Colloquium on Analysis and numerics of partial differential equations, in memory of Enrico Magenes, Pavia, 2-4 November
• PhD viva, 15 September
• Workshop on Advances in Computational Wave Propagation, University College London, 2-3 September
• Pro*Doc summer retreat, Disentis, Switzerland, 17-19 August
• Finite Element Fair/Rodeo/Circus, University of Chicago Center, Paris, 3-4 June
• Swiss Numerics Colloquium, Università della Svizzera Italiana, Lugano, Switzerland, 6 May
• Reading, 5-9 April
• SamHyp2011 - Numerical methods for hyperbolic equations, Zürich, 18-19 February
2010
• Workshop on Next Generation Numerical Methods for Computational Wave Propagation, Cambridge, 17-18 September
• ESF conference on Highly Oscillatory Problems: From Theory to Applications, Isaac Newton Institute, Cambridge, 12-17 September
• Zürich Summer School 2010 on Sparse Tensor Discretisations of High-Dimensional Problems, Zürich, 23-27 August
• Pro*Doc summer retreat, Disentis, Switzerland, 18-21 August
• ACE'10 6th Workshop on Advanced Computational Electromagnetics, ETH Zürich, 5-7 July
• Workshop on Non-Standard Numerical Methods for PDE's, Pavia, 29 June-2 July
• DSPDEs'10, joint SIAM/RSME-SCM-SEMA Meeting on Emerging Topics in Dynamical Systems and PDEs, Barcelona, 31 May-4 June
• Swiss Numerics Colloquium, ETH Zürich, 16 April
• Oberwolfach workshop on Computational Electromagnetism and Acoustics, 14-20 February
• WONAPDE 2010, Universidad de Concepción, Chile, 11-15 January
2009
• Seminar at the Chinese University of Hong Kong, 9 September
• Chinese University of Hong Kong, September-October
• Pro*Doc summer retreat, Disentis, Switzerland, 16-19 August
• Mafelap 2009, Brunel University, London, 9-12 June
• Swiss Numerics Colloquium, Basel, 24 April