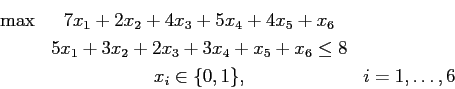Next: Capacità di una rete
Up: Variabili
Previous: Investimento di capitale
Un rapinatore si introduce furtivamente in una gioielleria avendo a disposizione un sacco con capacità di 8 chili. Trova a portata di mano 6 oggetti il cui valore 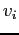 in migliaia di è rispettivamente: 7, 2, 4, 5, 4 e 1; il loro peso
in migliaia di è rispettivamente: 7, 2, 4, 5, 4 e 1; il loro peso 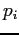 invece è rispettivamente di 5, 3, 2, 3, 1 e 1 chili. Potendo utilizzare il solo sacco a disposizione per trasportare la refurtiva, il ladro vuole effettuare la scelta di oggetti che massimizzi il valore complessivo.
Possiamo rappresentare il problema in due modi. Un primo modo è di tipo insiemistico. Sia
invece è rispettivamente di 5, 3, 2, 3, 1 e 1 chili. Potendo utilizzare il solo sacco a disposizione per trasportare la refurtiva, il ladro vuole effettuare la scelta di oggetti che massimizzi il valore complessivo.
Possiamo rappresentare il problema in due modi. Un primo modo è di tipo insiemistico. Sia
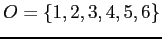 , la nostra variabile decisionale è data dall'insieme
, la nostra variabile decisionale è data dall'insieme 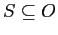 ; vogliamo trovare un sottoinsieme
; vogliamo trovare un sottoinsieme 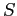 tale che
tale che
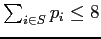 , e che massimizzi
, e che massimizzi
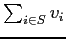 . In alternativa, utilizzando variabili matematiche, possiamo introdurre una variabile di scelta
. In alternativa, utilizzando variabili matematiche, possiamo introdurre una variabile di scelta 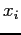 per ogni oggetto
per ogni oggetto 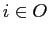 che vale 1 se e solo se l'oggetto i viene scelto e 0 altrimenti. Le variabili decisionali sono di tipo ``logico", ovvero per ogni oggetto dobbiamo decidere se includerlo o meno nella soluzione:
che vale 1 se e solo se l'oggetto i viene scelto e 0 altrimenti. Le variabili decisionali sono di tipo ``logico", ovvero per ogni oggetto dobbiamo decidere se includerlo o meno nella soluzione: 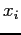 varrà 1 se l'oggetto
varrà 1 se l'oggetto 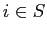 e 0 altrimenti. In questo modo il problema viene rappresentato dal seguente modello:
e 0 altrimenti. In questo modo il problema viene rappresentato dal seguente modello:
A volte si ha la necessità di effettuare una scelta tra un insieme finito di valori, pertanto la variabile che rappresenta tale scelta non rientra in nessuna delle categorie menzionate sopra e parliamo di variabile a valori discreti. Il contesto tipico è quello delle reti di telecomunicazione.



Next: Capacità di una rete
Up: Variabili
Previous: Investimento di capitale