Regole e vincoli

Il secondo elemento fondamentale di un modello matematico di ottimizzazione è dato dalle regole che caratterizzano il sistema da modellare. Nel caso del coltivatore, le regole riguardano il consumo di semi di lattuga, di piante di pomodoro, di tuberi e di stallatico. Per ognuna di queste risorse, la quantità utilizzata non può superare la quantità disponibile. L'aver individuato le variabili decisionali rende semplice quantificare il consumo di risorse come conseguenza delle decisioni prese. Per esempio, sapendo di dover coltivare 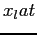$x_lat$ ettari di lattuga la quantità di semi necessaria è data da 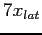$7 x_{lat}$, ovvero dalla quantità di semi necessaria per un ettaro moltiplicato per il numero di ettari. Il vincolo che esprime la regola sul limite di utilizzo di semi è quindi:

$$7 x_{lat} \leq 70.$$

In modo analogo possiamo procedere per le altre regole che sono dello stesso tipo:

$$20000 x_{pom} \leq 50000$$

$$3 x_{pat} \leq 18$$

$$10 x_{lat} + 20 x_{pom} + 15 x_{pat} \leq 180.$$

Si noti come nell'ultimo vincolo, essendo lo stallatico una risorsa condivisa tra più coltivazioni, compaiano le tre variabili decisionali, ognuna con i propri coefficienti di consumo di risorsa. Il modello deve includere anche un vincolo che riguarda l'altra risorsa condivisa che è il terreno:

$$x_{lat} + x_{pom} + x_{pat} \leq 13.$$