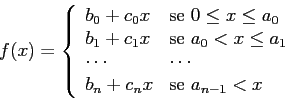Next: Esercizi
Up: Funzioni obiettivo
Previous: Localizzazione di stazioni radio
Prima dell'avvento della deregolamentazione nel mondo della telefonia italiana vigeva la seguente tariffa per le utenze domestiche: per i primi 140 scatti il costo era di 50 lire, dal 141-esimo scatto al 220-esimo il costo era di 207 lire e per i successivi 127 lire. In figura 6 viene rappresentato uno schema di tale funzione costo, dove 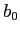 rappresenta il costo fisso (per esempio il costo del canone bimestrale).
rappresenta il costo fisso (per esempio il costo del canone bimestrale).
fig. 6: vecchia tariffa sip per utenze domestiche
Quindi, indicando con 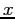 il numero di scatti e con
il numero di scatti e con 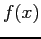 la funzione costo, formalmente abbiamo:
la funzione costo, formalmente abbiamo:
dove 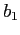 e
e 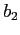 sono i valori dell'intercetta delle rette rossa e verde in figura. Volendo utilizzare questa funzione costo in un problema di ottimizzazione ci troveremmo davanti alla difficoltà di avere a che fare con una funzione obiettivo non lineare, anche se lineare a tratti. Vi è un modo di trattare queste funzioni ricorrendo a modelli di programmazione lineare intera. L'idea è di trattare separatamente i tre intervalli
sono i valori dell'intercetta delle rette rossa e verde in figura. Volendo utilizzare questa funzione costo in un problema di ottimizzazione ci troveremmo davanti alla difficoltà di avere a che fare con una funzione obiettivo non lineare, anche se lineare a tratti. Vi è un modo di trattare queste funzioni ricorrendo a modelli di programmazione lineare intera. L'idea è di trattare separatamente i tre intervalli ![$[0,140]$](img161.png) ,
, ![$(140,220]$](img162.png) ,
, ![$(220,M]$](img163.png) con
con 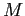 costante opportunamente grande. Introduciamo delle variabili continue
costante opportunamente grande. Introduciamo delle variabili continue 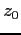 ,
, 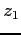 e
e 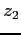 che indicano quanti scatti vengono consumati nella prima fascia, nella seconda e nella terza, rispettivamente. Dobbiamo anche introdurre un meccanismo che impedisca consumare gli scatti di un intervallo se prima non sono stati esauriti quelli dell'intervallo precedente. Questo viene fatto introducendo delle variabili 0-1, una per ogni intervallo, (
che indicano quanti scatti vengono consumati nella prima fascia, nella seconda e nella terza, rispettivamente. Dobbiamo anche introdurre un meccanismo che impedisca consumare gli scatti di un intervallo se prima non sono stati esauriti quelli dell'intervallo precedente. Questo viene fatto introducendo delle variabili 0-1, una per ogni intervallo, (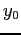 ,
, 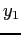 e
e 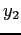 ) che valgono 1 solo se abbiamo iniziato a consumare qualche scatto nell'intervallo a cui si riferiscono. La funzione obiettivo e i vincoli che realizzano il meccanismo a cui abbiamo accennato sono:
) che valgono 1 solo se abbiamo iniziato a consumare qualche scatto nell'intervallo a cui si riferiscono. La funzione obiettivo e i vincoli che realizzano il meccanismo a cui abbiamo accennato sono:
Si noti che se per esempio 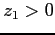 allora
allora 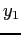 deve risultare uguale a 1, il che implica che
deve risultare uguale a 1, il che implica che 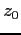 deve essere uguale a 140, quindi dobbiamo aver esaurito tutti gli scatti dell'intervallo precedente.
Volendo generalizzare quanto visto nel caso dell'esempio della tariffa telefonica ad un contesto più generale, consideriamo la seguente funzione lineare a tratti da minimizzare, la cui rappresentazione grafica è data in figura 7:
deve essere uguale a 140, quindi dobbiamo aver esaurito tutti gli scatti dell'intervallo precedente.
Volendo generalizzare quanto visto nel caso dell'esempio della tariffa telefonica ad un contesto più generale, consideriamo la seguente funzione lineare a tratti da minimizzare, la cui rappresentazione grafica è data in figura 7:
???? VOGLIAMO GENERALIZZARE?????
Vi sono situazioni particolari in cui non è necessario introdurre variabili 0,1 per indurre il meccanismo di sequenzialità nella crescita delle variabili 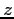 . Uno di questi è per esempio la minimizzazione di una funzione lineare a tratti convessa, di cui riportiamo un esempio in figura 8.
. Uno di questi è per esempio la minimizzazione di una funzione lineare a tratti convessa, di cui riportiamo un esempio in figura 8.
fig.8: funzione convessa lineare a tratti
Con una simile funzione è abbastanza semplice intuire che vi è maggior vantaggio a utilizzare la parte iniziale della funzione, con costi unitari più bassi, prima di passare a quelle successive. Formalmente possiamo vedere che tali funzioni possono venire rappresentate con la tecnica delle funzioni obiettivo di tipo bottleneck vista nel primo capitolo. Sia data la funzione convessa lineare a tratti:
Se consideriamo le varie rette anche al di fuori del campo di definizione degli intervalli, vediamo che la funzione è data sempre dalla retta più in alto, quindi:



Next: Esercizi
Up: Funzioni obiettivo
Previous: Localizzazione di stazioni radio
![]() il numero di scatti e con
il numero di scatti e con ![]() la funzione costo, formalmente abbiamo:
la funzione costo, formalmente abbiamo:
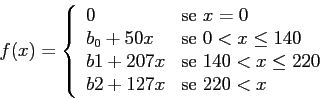
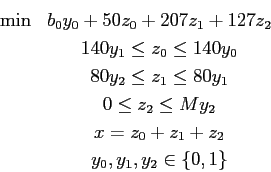
![]() . Uno di questi è per esempio la minimizzazione di una funzione lineare a tratti convessa, di cui riportiamo un esempio in figura 8.
. Uno di questi è per esempio la minimizzazione di una funzione lineare a tratti convessa, di cui riportiamo un esempio in figura 8.