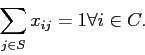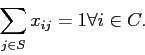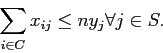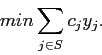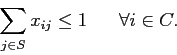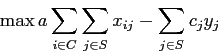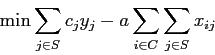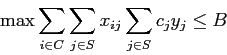Localizzazione di stazioni radio base

Nel pianificare una rete di telefonia cellulare bisogna installare le antenne delle stazioni radio-base scegliendo tra un insieme di siti candidati 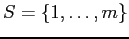$S=\{1,\ldots,m\}$ in modo da servire un insieme di clienti 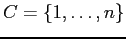$C=\{1,\ldots,n\}$. Per raggiungere un cliente 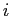$i$ l'antenna installata in 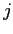$j$ deve trasmettere con una potenza 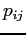$p_{ij}$. Vogliamo decidere dove installare le stazioni radio base in modo da minimizzare la massima potenza emessa. Le variabili in gioco sono quelle che rappresentano la scelta di dove installare le antenne: 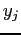$y_j$ vale 1 se una antenna viene messa nel sito 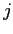$j$ e 0 altrimenti. Inoltre avremo le variabili 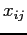$x_{ij}$ che assegnano 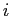$i$ clienti alle antenne, (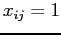$x_{ij} =1$ se il cliente 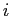$i$ viene servito dalla antenna 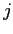$j$ e 0 altrimenti). I vincoli riguardano il fatto che ogni cliente deve essere servito:

$$\sum_{j\in S} x_{ij} = 1 \forall i \in C.$$

Inoltre dobbiamo introdurre dei vincoli che rendono coerente l'assegnamento di un cliente con la scelta delle antenne installate, pertanto un vincolo che imponga di non assegnare clienti alle stazioni non attivate. Abbiamo due modi di scrivere questo vincolo: il primo modo è più sintetico dato che considera assieme tutti i clienti che possono venire collegati a una determinata antenna:

$$\sum_{i\in C} x_{ij} \leq n y_j \forall j\in S.$$

Si noti come questo tipo di vincoli richiami l'implicazione generalizzata vista precedentemente. Il secondo modo di rappresentare i vincoli di coerenza considera ogni singola coppia cliente-antenna:

$$x_{ij} \leq y_j \forall i\in C, \forall j\in S.$$

Anche in questo caso si tratta di una implicazione: se 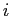$i$ è assegnato a 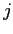$j$ allora 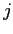$j$ deve avere una antenna installata. Questi due modi di rappresentare i vincoli di coerenza sono equivalenti dal punto di vista modellistico. Se consideriamo invece l'efficienza di soluzione, il secondo tipo di formulazione, nonostante il maggior numero di vincoli, permette ai solutori di problemi di Programmazione Lineare Intera di essere più efficienti. Consideriamo ora la funzione obiettivo che comporta la minimizzazione del massimo livello di potenza emesso:

$$\min \max_{i\in C, j\in S} p_{ij}x_{ij}.$$

La funzione obiettivo vera e propria ( 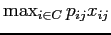$\max_{i\in C} p_{ij}x_{ij}$) che si intende minimizzare è evidentemente non lineare, ma con opportuni accorgimenti può venire ``linearizzata". Per fare ciò è necessario introdurre una variabile d che ha il compito di determinare il valore della funzione obiettivo. Pertanto ora la funzione obiettivo si riduce a:

$$\min d.$$

Ora bisogna aggiungere dei vincoli in modo da legare la variabile d con il resto della soluzione:

$$d \geq p_{ij}x_{ij} \;\;\;\;\; \forall i\in C, \forall j\in S.$$

In questo modo la variabile d non può valere meno del massimo valore di potenza tra ogni cliente e l'antenna a cui è assegnato, però il segno dell'ottimizzazione (minimo) spingerà d ad assumere esattamente il valore del massimo.

Molto spesso nell'affrontare un problema reale di ottimizzazione non ci si pone un solo obiettivo, ma potrebbero essercene vari, spesso in contrasto fra loro. Si rientra nel caso della programmazione a molti obiettivi. Vediamo due modi di affrontare questi casi riprendendo una variante dell'esempio di prima. Esempio: localizzazione di stazioni radio base considerando il costo di realizzazione Nell'esempio precedente ci eravamo concentrati sugli aspetti legati alla potenza, adesso invece consideriamo il costo della realizzazione della rete ponendoci l'obiettivo di minimizzarlo. A differenza dell'esempio precedente quindi consideriamo un costo di installazione cj>0 per ciascun sito candidato j. I vincoli del problema sono invariati, mentre la funzione obiettivo considera i costi ed è:

$$min \sum_{j\in S} c_j y_j.$$

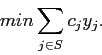
Consideriamo ora una situazione in cui non si richiede la copertura totale dell'insieme degli utenti, pertanto il vincolo di copertura da uguaglianza diventa disuguaglianza:

$$\sum_{j\in S} x_{ij} \leq 1 \;\;\;\;\;\; \forall i\in C.$$

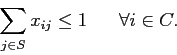
È evidente che il problema di ottimizzazione che minimizza i costi di installazione senza il vincolo di copertura di tutti gli utenti ha come soluzione ottima la soluzione nulla. Possiamo quindi porci come secondo obiettivo quello di massimizzare il numero di clienti serviti, che è in contrasto con quello di minimizzare il costo.

Vi sono due modi di considerare due (o più) funzioni obiettivo. Un primo modo tenta di ridurre le due funzioni ad una stessa scala di valori, considerando entrambi i criteri su uno stesso piano e includendoli in una unica funzione di utilità. Nell'esempio delle rete cellulare introduciamo un parametro a che quantifica in termini economici il vantaggio di avere un nuovo utente collegato. La funzione di utilità quindi diventa:

$$\max a \sum_{i\in C}\sum_{j\in S} x_{ij} - \sum_{j\in S} c_j y_j$$

o alternativamente

$$\min \sum_{j\in S} c_j y_j - a \sum_{i\in C}\sum_{j\in S} x_{ij}$$

Si noti che il contributo alla funzione di utilità dovuto al numero di utenti serviti è negativo, dato che il segno di ottimizzazione è di minimo. Inoltre la scelta del parametro a deve essere tale da privilegiare la copertura rispetto ai costi, per non ottenere la soluzione nulla, cosa abbastanza probabile con valori di a troppo piccoli.

Il secondo modo di trattare problemi con più obiettivi è quello di fissare dei valori di riferimento per alcuni obiettivi da mettere esplicitamente nei vincoli del problema e lasciare nella funzione obiettivo una unica funzione. Sempre nel caso dell'installazione di antenne per stazioni radio base, si potrebbe fissare un limite massimo per le spese di installazione, chiamiamolo B, e massimizzare la copertura degli utenti. Pertanto la formulazione sarebbe:

$$\max \sum_{i\in C} \sum_{j\in S} x_{ij} \sum_{j\in S} c_j y_j \leq B$$

oltre ai vincoli già descritti precedentemente.