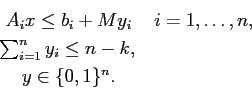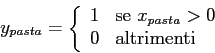
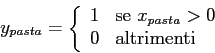
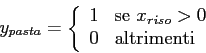
I vincoli di esclusione sono un caso particolare di vincolo logico (or esclusivo). Vediamone altri come per esempio le implicazioni: se la variabile ![]() vale 1, allora deve valere 1 anche la variabile
vale 1, allora deve valere 1 anche la variabile ![]() ; vedendo le variabili in accordo al loro significato logico il vincolo rappresenta l'implicazione
; vedendo le variabili in accordo al loro significato logico il vincolo rappresenta l'implicazione
![]() . Ricordando il significato dell'implicazione, tra tutte le configurazioni di valori delle variabili quello che dobbiamo vietare è
. Ricordando il significato dell'implicazione, tra tutte le configurazioni di valori delle variabili quello che dobbiamo vietare è ![]() , che viene tradotto in termini matematici come:
, che viene tradotto in termini matematici come:
Fino ad ora abbiamo visto esempi di problemi in cui la regione ammissibile è descritta da un poliedro convesso, o è data dai punti interi racchiusi in un poliedro convesso. Potrebbero verificarsi casi in cui tale proprietà viene meno e la regione ammissibile è data da un poliedro non convesso. Consideriamo ad esempio la regione ammissibile descritta in figura 2.
fig. 2 esempio di regione ammissibile non convessa
La regione in figura può essere descritta come unione di due poliedri convessi ![]() e
e ![]() , come evidenziato dalla figura 3.
, come evidenziato dalla figura 3.
fig. 3: decomposizione del poliedro
Il poliedro ![]() è dato da
è dato da
![]() , mentre
, mentre
![]() . Per fare l'intersezione dei due poliedri sappiamo che basta che tutti i vincoli di
. Per fare l'intersezione dei due poliedri sappiamo che basta che tutti i vincoli di ![]() e di
e di ![]() valgano contemporaneamente, se invece ci interessa l'unione dobbiamo imporre che almeno uno dei due gruppi di vincoli valga. In primo luogo osserviamo che alcuni vincoli sono comuni ai due poliedri, in particolare
valgano contemporaneamente, se invece ci interessa l'unione dobbiamo imporre che almeno uno dei due gruppi di vincoli valga. In primo luogo osserviamo che alcuni vincoli sono comuni ai due poliedri, in particolare
![]() , quindi di fatto di questi vincoli possiamo anche fare l'intersezione, mentre quelli che caratterizzano più propriamente le due regioni ammissibili sono
, quindi di fatto di questi vincoli possiamo anche fare l'intersezione, mentre quelli che caratterizzano più propriamente le due regioni ammissibili sono
![]() per quel che riguarda
per quel che riguarda ![]() e
e
![]() per quel che riguarda
per quel che riguarda ![]() . Dobbiamo fare in modo che nella nostra formulazione almeno uno di questi due vincoli valga, quindi, considerando il problema dal punto di vista opposto, questo significa che al massimo uno di questi due vincoli può venire reso ridondante. Annullare uno di questi vincoli significa traslarlo di una quantità sufficiente da fargli includere tutta la regione ammissibile dell'altro poliedro, come evidenziato in figura 4.
. Dobbiamo fare in modo che nella nostra formulazione almeno uno di questi due vincoli valga, quindi, considerando il problema dal punto di vista opposto, questo significa che al massimo uno di questi due vincoli può venire reso ridondante. Annullare uno di questi vincoli significa traslarlo di una quantità sufficiente da fargli includere tutta la regione ammissibile dell'altro poliedro, come evidenziato in figura 4.
fig. 4: traslazione dei vincoli
Per poter effettuare questa operazione di annullamento di al più un vincolo (o un gruppo di vincoli) tra i due individuati, introduciamo le variabili 0-1 ![]() e
e ![]() che valgono 1 se decidiamo di annullare il vincolo relativo a
che valgono 1 se decidiamo di annullare il vincolo relativo a ![]() o a
o a ![]() , rispettivamente. La formulazione della regione in figura 2 risulta quindi:
, rispettivamente. La formulazione della regione in figura 2 risulta quindi:
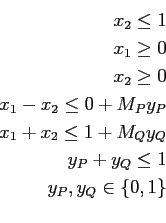
Il vincolo
![]() consente di annullare al più uno dei due gruppi di vincoli. La scelta delle due costanti
consente di annullare al più uno dei due gruppi di vincoli. La scelta delle due costanti ![]() e
e ![]() deve essere tale da garantire che la regione ammissibile sia completamente contenuta dal vincolo traslato. Nel nostro caso quindi
deve essere tale da garantire che la regione ammissibile sia completamente contenuta dal vincolo traslato. Nel nostro caso quindi ![]() e
e ![]() .
.
Un caso particolare di applicazione della tecnica dei vincoli disgiuntivi riguarda i problemi di scheduling di lavori su macchine. Poniamoci il problema di processare ![]() lavori
lavori ![]() su
su ![]() macchine denotate da
macchine denotate da ![]() . Ogni lavoro deve essere eseguito prima sulla macchina 1, poi sulla 2, e così via fino ad essere eseguito al termine sull'ultima macchina
. Ogni lavoro deve essere eseguito prima sulla macchina 1, poi sulla 2, e così via fino ad essere eseguito al termine sull'ultima macchina ![]() . Il tempo di esecuzione del lavoro
. Il tempo di esecuzione del lavoro ![]() sulla macchina
sulla macchina ![]() è dato da
è dato da
![]() e
e ![]() . Le varie macchine possono eseguire un lavoro alla volta e i lavori su ogni macchina devono essere eseguiti fino al termine, cioè non possono essere interrotti e ripresi. Il problema consiste nella determinazione del sequenziamento dei vari lavori sulle diverse macchine con l'obiettivo di minimizzare il tempo di fine dell'ultimo lavoro (in gergo chiamato makespan). Per stabilire il sequenziamento abbiamo bisogno di variabili
. Le varie macchine possono eseguire un lavoro alla volta e i lavori su ogni macchina devono essere eseguiti fino al termine, cioè non possono essere interrotti e ripresi. Il problema consiste nella determinazione del sequenziamento dei vari lavori sulle diverse macchine con l'obiettivo di minimizzare il tempo di fine dell'ultimo lavoro (in gergo chiamato makespan). Per stabilire il sequenziamento abbiamo bisogno di variabili ![]() che fissano il tempo di inizio del lavoro j sulla macchina
che fissano il tempo di inizio del lavoro j sulla macchina ![]() . Con queste variabili è semplice formulare i vincoli che riguardano la sequenza di lavorazione di ogni singolo lavoro:
. Con queste variabili è semplice formulare i vincoli che riguardano la sequenza di lavorazione di ogni singolo lavoro:
Generalizzando la tecnica dei vincoli disgiuntivi vista per il caso della regione non convessa e per lo scheduling, consideriamo il problema di determinare una soluzione che soddisfi almeno ![]() (
(
![]() ) dei vincoli:
) dei vincoli: