Dieta

Si consideri il problema di determinare la dieta giornaliera avendo a disposizione vari cibi ognuno con le proprie caratteristiche nutrizionali. Prendiamo ad esempio la seguente tabella con i tipici cibi della mensa del Politecnico di Milano:

Tabella: menu della mensa e apporti calorici

Cibo Pasta	Riso	Fettina di lonza	Carote	Patate	Pera
Calorie per hg	300	250	200	70	180	100

Il fabbisogno imposto dal dietologo è di almeno 700 calorie. Per esprimere il vincolo del dietologo introduciamo delle variabili 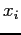$x_i$ per i vari cibi 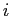$i$ che rappresentano la quantità di cibo assunta (in hg) e il vincolo sarà:

$$300 x_{pasta} + 250 x_{riso} + 200 x_{lonza} + 70 x_{carote} + 180 x_{patate} + 100 x_{pera} \geq 700$$

Talvolta risulta utile trasformare i vincoli di maggiore o uguale (come quello visto nell'esempio della dieta) o di minore o uguale (come quelli visti nell'esempio del coltivatore) in vincoli equivalenti di uguaglianza. La trasformazione necessita dell'introduzione di una nuova variabile per vincolo che rappresenta il margine rispetto al fabbisogno (nel caso di 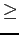$\geq$) o l'avanzo di risorse rispetto alla disponibilità (nel caso di 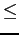$\leq$). Prendiamo il caso del vincolo sulla disponibilità di stallatico nel problema del coltivatore, volendolo trasformare in uguaglianza abbiamo:

$$10 x_{lat} + 20 x_{pom} + 15 x_{pat} + x_s = 180$$

dove la nuova variabile 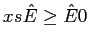$xsÊ\geqÊ0$ è detta variabile di scarto e dà la misura di quanta risorsa rimane a disposizione. Se consideriamo il vincolo sul fabbisogno della dieta, volendolo trasformare in uguaglianza abbiamo:

$$300 x_{pasta} + 250 x_{riso} + 200 x_{lonza} + 70 x_{carote} + 180 x_{patate} + 100 x_{pera} - x_s = 700$$

dove la variabile di scarto 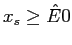$x_s \geqÊ0$ dà la misura di quanto stiamo eccedendo il fabbisogno calorico.

Una importante classe di vincoli è rappresentata dai vincoli di flusso che emergono in moltissimi campi applicativi, tanto che una parte del corso è dedicata esplicitamente ai metodi di soluzione di questo tipo di problemi. Prendiamo in esame un semplice esempio.