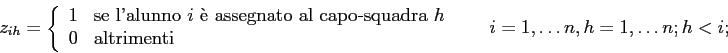
Siccome questo genere di formulazione ammette un elevato numero di soluzioni equivalenti (non c'e' nessuna differenza ad assegnare una squadra a un colore o a un altro), si possono introdurre variabili completamente diverse. Invece che assegnare gli alunni a una squadra, li si assegna a un capo-squadra (l'alunno di indice minimo).
Le variabili sono:
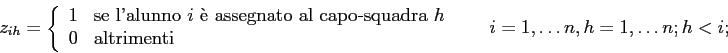
Permangono le variabili ![]() che vengono interpretate in questo modo:
che vengono interpretate in questo modo:

I vincoli sono:
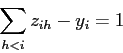
I vincoli di assegnamento a colori di amici si modificano come segue:
La funzione obiettivo rimane invariata.