In questa seconda variante dobbiamo considerare due veicoli e quindi due insiemi variabili di flusso riferite al primo e al secondo veicolo:
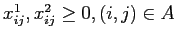 .
Per entrambi gli insiemi di variabili imponiamo la conservazione del flusso:
.
Per entrambi gli insiemi di variabili imponiamo la conservazione del flusso:
Il vincolo che almeno un veicolo passi per un arco diventa:
Avendo due veicoli, a differenza che nel caso di un singolo veicolo, è indispensabile imporre che entrambi gli itinerari includano il nodo deposito (0).
Inoltre è necessario imporre la connessione degli itinerari, cosa che richiede un numero esponenziale di vincoli. Considerando un qualsiasi sottoinsieme di nodi 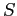 che non include il deposito 0, se un veicolo percorre archi all'interno di
che non include il deposito 0, se un veicolo percorre archi all'interno di 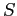 allora deve percorrere anche un arco con un estremo in
allora deve percorrere anche un arco con un estremo in 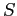 e uno non in
e uno non in 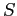 .
.
La funzione obiettivo minimizza la lunghezza del massimo itinerario. Sia 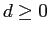 una opportuna variabile:
una opportuna variabile:





