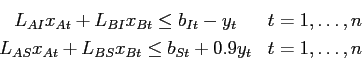Caseificio: suggerimenti per la variante

Bisogna introdurre un nuovo insieme di variabili non negative riguardanti la trasformazione del latte intero, giorno per giorno:

$$y_t = \mbox{litri di latte intero trasformato in latte scremato nel giorno $t$}(\geq 0) \;\;\;\;\; t=1,\ldots,n.$$

I vincoli sul consumo delle risorse () e () si trasformano in questo modo:

$$\begin{eqnarray*} & L_{AI} x_{At} + L_{BI} x_{Bt} \leq b_{It} - y_t & t=1,\ldots... ...{AS} x_{At} + L_{BS} x_{Bt} \leq b_{St} + 0.9 y_t & t=1,\ldots,n \end{eqnarray*}$$

Per considerare nella funzione obiettivo il costo fisso dobbiamo anche introdurre un insieme di variabili 0-1 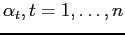$\alpha_t, t=1,\ldots,n$, il cui significato è:

$$\alpha_t = \left\{ \begin{array}{ll} 1 & \mbox{se il proce... ...el giorno $t$} \\ 0 & \mbox{altrimenti} \end{array} \right.$$

Sono inoltre necessari dei vincoli per legare le variabili 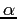$\alpha$ alle variabili $y$:

$$y_t \leq b_{It} \alpha_t, \;\;\;\;\;\;\; t=1,\ldots,n$$

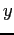Si noti che 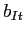$b_{It}$ è la massima quantità di latte intero disponibile nel giorno 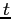$t$, quindi, in mancanza di indicazioni più stringenti, è anche la massima quantità di latte intero trasformabile nel giorno $t$.

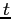La funzione obiettivo a questo punto è:

$$\begin{eqnarray*} \min &c_A \sum_{t=1}^{n} z_{At} + c_B \sum_{t=1}^n z_{Bt} + c_T \sum_{t=1}^n y_{t} + F \sum_{t=1}^n \alpha_{t} \end{eqnarray*}$$