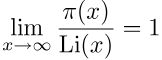Intorno al 1850 Chebyshev mostrò che, per x sufficientemente grande, valgono le disuguaglianze

In altre parole, l'errore relativo che si commette rimpiazzando la funzione  con l'integrale logaritmico non supera l'11%, per valori grandi dell'argomento. Chebyshev mostrò anche che, se il rapporto

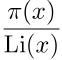
tende a un limite per x tendente all'infinito, questo limite deve essere 1. Che il limite esiste è il contenuto del

Teorema dei numeri primi (Hadamard, de la Vallée Poussin, 1896)