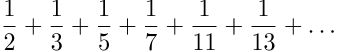
Osservazioni empiriche mostrano che, a piccola scala, la distribuzione dei primi è estremamente irregolare, mentre a grande scala mostra un andamento regolare.

Eulero dimostrò nel 1737 che la serie

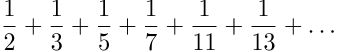
i cui addendi sono i reciproci dei primi diverge; in altre parole, al crescere di n, le somme

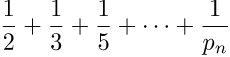
dove  indica l'n-esimo primo, crescono senza limite. I numeri primi quindi non solo sono infiniti, ma sono anche "molti".