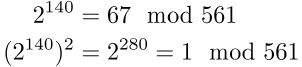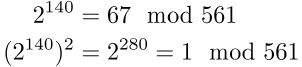Quello che abbiamo mostrato dimostrando il Fatto 2 è
più in generale che, se p è primo, le sole radici
quadrate di 1 modulo p sono 1 e -1. Questa osservazione può
servire a dimostrare direttamente che alcuni numeri non sono primi. Ad
esempio, per mostrare che 561 non è primo si può notare che
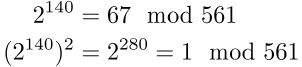
e quindi 1 ha una terza radice quadrata (67) modulo 561.
Più in generale si può mostrare che, se
p è primo, una equazione algebrica di grado n ha al
più n soluzioni modulo p. Anche questa generalizzazione
è utile nei test di primalità.